硬核音频系列文章列表:
- 硬核音频系列(一)—— 声音信息的表示:基础概念扫盲,PCM 编码方式
- 硬核音频系列(二)—— 音频文件编解码格式:动手实现 adpcm 解码器
- 硬核音频系列(三)—— 线性淡入淡出:算法思路、实现与优化方法描述
硬核音频系列第三篇,聊聊淡入淡出怎么搞。
音频淡入淡出概述
淡入淡出(fade in & fade out)可以实现音频音量在开始播放时渐强,以及停止播放时渐弱,防止声音切换带来的音量突变。实现淡入淡出重点要解决的问题,在于如何调节 PCM 数据的音量大小。一开始我天真的认为,只要把每一个采样值加上或减去某个数就可以了,但事情可没这么简单,加上一个数虽然能让采样值增大,但却会造成声音波形失真,并不可行。
淡入淡出本质上是对音频音量作线性变换,可以通过对每个采样值乘上一个变换系数实现,并且这个系数应该是个随时间变化量,如最简单的线性函数 y = kx。但在实际应用中,处理范围内 y 需在 0~1 之间变化,对应音量从零到原始值,自变量 x 可看作某个音频位置(时间、采样序号等),假设需要在 x = 500 位置处音量渐变到最大,则算出 k = 1/500。
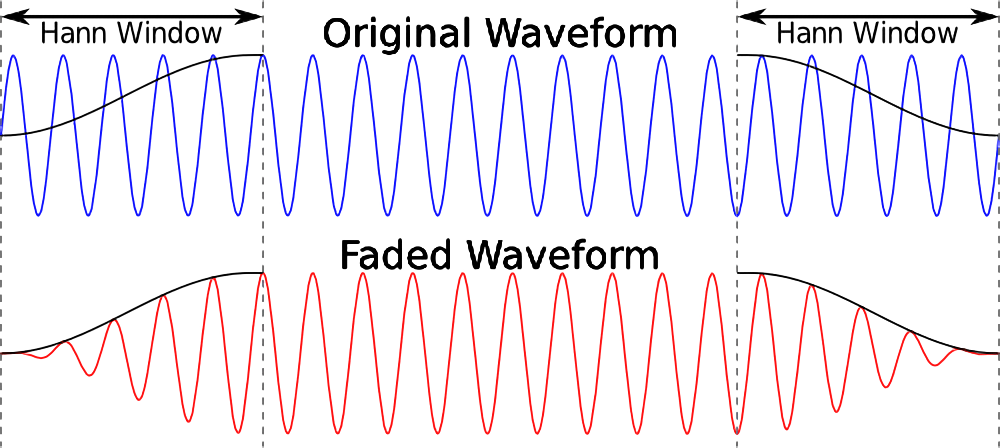
算法原理(以淡入为例)
对给定的 t1-t2 时间区间的单声道音频采样进行淡入操作(t1一般取0),先把时间统一换算为采样数,作为基本单位,然后计算已处理的采样数占待处理采样总数比例,得到出下一采样对应的变换系数,再与采样相乘,得到输出采样值。
举个栗子,要对 100 个采样从头开始、依次进行淡入处理,在第 0、50、70 个采样处的计算方式如下:
factor = 0 / 100;
out_sample[0] = out_sample[0] * factor;
factor = 50 / 100;
out_sample[50] = out_sample[50] * factor;
factor = 70 / 100;
out_sample[70] = out_sample[70] * factor;
值得注意的是,变换系数为 0~1 的小数,在实际 C 编程中,为了避免浮点运算,通常把上面两步计算通过一条表达式完成,先计算分子乘法再算分母除法:
out_sample[0] = (out_sample[0] * 0) / 100;
out_sample[50] = (out_sample[50] * 50) / 100;
out_sample[70] = (out_sample[70] * 70) / 100;
综上,对算法步骤进行整理,得到以下计算流程:
- 通过采样率和声道数计算开始时刻、结束时刻、总处理时长对应的采样数
start_sample_pos、stop_sample_pos、fade_samples_count=stop_sample_pos-start_sample_pos - 计算已处理采样数:
done_sample_count = cur_sample_pos - start_sample_pos - 计算表达式分子乘法,得到中间变量:
tmp = out_sample * done_sample_count - 计算表达式分母除法,得到输出采样值:
out_sample = tmp / fade_samples_count - 更新当前采样位置:
cur_sample_pos++
对应的程序运行日志:
[cal] factor = done_sample_count/fade_samples_count = 4917/96000
[cal] factor = done_sample_count/fade_samples_count = 4918/96000
[cal] factor = done_sample_count/fade_samples_count = 4919/96000
[cal] factor = done_sample_count/fade_samples_count = 4920/96000
[cal] factor = done_sample_count/fade_samples_count = 4921/96000
[cal] factor = done_sample_count/fade_samples_count = 4922/96000
[cal] factor = done_sample_count/fade_samples_count = 4923/96000
性能优化
对于分母除法, fade_samples_count 只需计算一次,后面不变,而分子需要每次动态计算乘法,比较悲催的是即使就这点计算量,也并不是所有硬件都能 hold 得住,在 cpu 资源紧张的硬件上运行乘除法,会消耗一定时间,甚至造成部分音频卡顿现象。
13758: 9802 ldr r0, [sp, #8]
1375a: 9903 ldr r1, [sp, #12]
1375c: 2300 movs r3, #0
1375e: 002a movs r2, r5
13760: f086 fe04 bl 9a36c <____aeabi_ldivmod_from_thumb>
13764: 2101 movs r1, #1
13766: 8030 strh r0, [r6, #0]
13768: 2018 movs r0, #24
从反汇编代码看出,我调试所用硬件架构没有除法指令,只能通过调用 <____aeabi_ldivmod_from_thumb> 实现计算除法。导致 cpu 占用过高,没办法所以要对算法进一步优化,主要是运算符的精简。
优化方案一 —— 移位替代分母除法
保持算法思路不变,将上述步骤 4 「计算表达式分母除法部分」中除法采用右移替换,但由于移位只适用乘除 2 的整数次幂,需要先把分母 fade_samples_count 向下取最接近的 2 次幂整数代替,如 96000 用 65536 替代,再进行右移操作:
tmp / 96000 => tmp / 65536 => tmp >> 16
相应的代码实现可以一步到位:计算除数对应二进制位数,再减一得到所需右移位数(96000 有 17 位二进制数,右移 16 位),代码实现:
...
int64_t tmp;
int bitcount = 0;
tmp = fade_samples_count;
while (tmp > 0)
{
tmp = tmp / 2;
bitcount++;
}
...
tmp = out_sample[i] * (int64_t)(f_info->cur_sample_pos-f_info->start_sample_pos);
out_sample[i] = tmp >> (bitcount-1);
...
这种替换能直接避免使用除法,实测性能提升 10 倍,但缺陷也很明显,那就是原操作数会损失不定量的数值(取决于与最近的 2 次幂有多靠近),从而造成计算结果误差。上面例子中 96000 直接少了 3w 多,具体效果表现为,淡入 3s 的音频实际只处理了 1s 多(可以通过其他手段补偿但还没尝试)。
因此本方案不适用于精确时间淡入淡出,只能算个大概,误差大小全看人品,但其实用于音乐播放影响不大。
优化方案二 —— 移位代替线性变化(用于提示音播放消 pop 声)
区分针对「听觉效果」与「硬件特性」的淡入淡出处理,可实现两套算法并根据具体情况调用 —— 播放音乐与播放提示音。短促的提示音甚至没必要通过动态计算线性变化系数处理,简陋的移位操作也许就能够起作用(效果待验证)。
前面所说的淡出淡入淡出效果,可适用于所有音频,能防止声音突然出现产生的突兀感,例如播放音乐时,人耳能明显感受到音量缓缓变化,暂且称为面向「听觉效果」的处理。而下面提到的第二种方案,适合对短促的提示音作淡入,可避免由于功放输入能量突变造成的 pop 音,处理目的更多的是面向「硬件特性」的优化,是另一种算法思路。
这实际上是对线性变换的一种简化,不再通过除法就计算变换系数,而是直接把采样值移位,达到近似的效果(或者看做固定几个变换系数的线性变换)。这时编程关注的重点在于移位操作本身 —— 从哪移到哪?在什么时机移?移多少位?
理论分析
考虑 16 位长度的采样值,在淡入处理时从最小音量到最大音量的过程中,每次移一位,需要经过最多 16 次左移操作,即移位总次数等于采样位宽,因此整个音频音量呈现出 16 级阶梯状变化,且每一级内采样点的音量是前一级的 2 倍,相比线性变换方式,音量增加存在锯齿状。
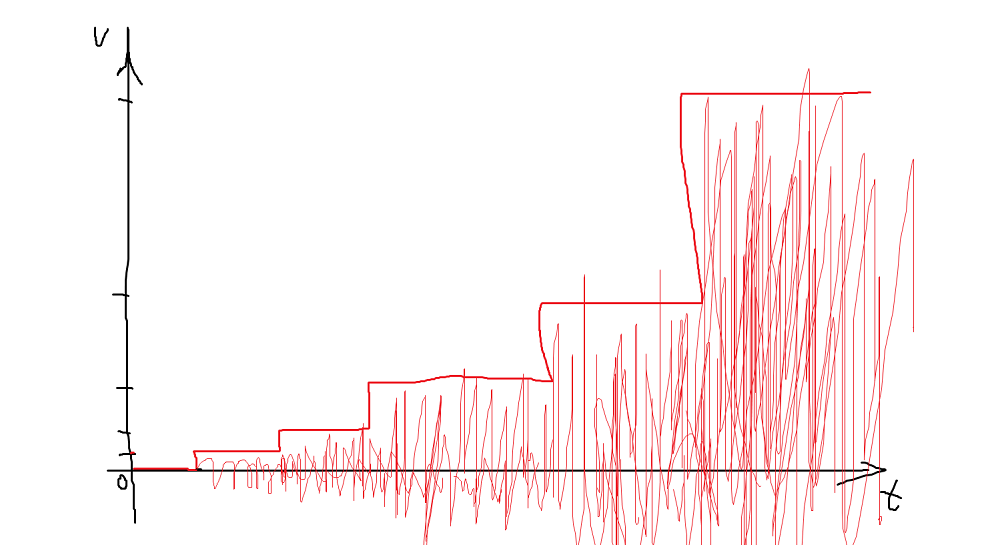
要保证 16 次移位后音量刚好达到最大,就要先计算每隔多久移位一次,可以通过总采样数 fade_samples_count 除以 16 得到(每一级内的采样数),每当达到一个移位间隔,执行一次移位。例如需要处理 1600 个采样,就是每 100 个采样移一位。
利用整除可以判断当前采样处于第几级,并通过右移递减的方式模拟左移递增,达到数据「一位一位冒出来」的效果,示意代码:
level = fade_samples_count / 16;
while (cur_sample_pos < stop_sample_pos)
{
tmp = cur_sample_pos / level;
out_sample[i] = out_sample[i] >> (16 - tmp);
}
同样,循环体中的除法必须干掉,同样使用移位代替整除,但你懂得,还是先要把除数近似到 2 次幂(计算二进制位数一步到位),并且由于截断误差原因,一部分采样数被舍弃掉,算出来的最大 level 或许达不到 16 级,音量级数变化范围改为 0 ~ bitcount,改写代码:
level = fade_samples_count / 16;
tmp = level;
while (tmp > 0)
{
tmp = tmp / 2;
bitcount++;
}
while (cur_sample_pos < stop_sample_pos)
{
tmp = cur_sample_pos >> bitcount;
out_sample[i] = out_sample[i] >> (bitcount - tmp);
}
随着移位二进制权值的递增,音量变化会越来越大,运行效果听起来便是:前面一大段时间音量增大幅度都很小,最后一小段音量急剧上升,听音乐还是有点突兀,但用于短促提示音可消除 pop 声并快速进入音频内容,当然了,将第一种算法的淡入时间改短也能达到相同效果。
参考资料
